Alle vorgestellten Aufteilungsmodelle (Aufteilungsmodelle in der Umlegung) sind in ihrer herkömmlichen Formulierung nicht in der Lage, Wechselwirkungen zwischen verschiedenen Verbindungen bei der fahrplanfeinen Umlegung zu berücksichtigen. Es kann allerdings von Nachteil sein, diesen Aspekt zu ignorieren.
Um Wechselwirkungen zu modellieren, definiert man Funktionen wi, welche die Wirkungen anderer Verbindungen auf eine Verbindung i beschreiben. Der Wertebereich von wi ist das Intervall [0,1]. Besitzt j keinerlei Wirkung auf i, gilt wi(j) = 0, bei völliger Übereinstimmung von i und j gilt wi(j) = 1, das heißt es ist auch stets wi(i) = 1.
Die folgenden Größen werden zur Berechnung von wi(j) herangezogen.
- die zeitliche Nähe beider Verbindungen im Hinblick auf Abfahrt und Ankunft
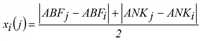
- der Vorteil von i gegenüber j in der empfundenen Reisezeit
yi(j) := ERZj - ERZi
- der Vorteil von i gegenüber j im Fahrpreis
zi(j) := FPj - FPi
Damit sei wi wie folgt definiert:
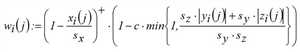 ,
,
wobei 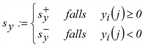 und
und 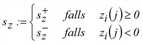
Die s > 0 sind interne Parameter zur Steuerung der Einflussbereiche der drei Größen. c ist eine Konstante, die die absolute Wirkung des zweiten Faktors kontrolliert und vom Benutzer innerhalb von [0,1] vorgegeben wird.
Der erste Faktor bildet die zeitliche Nähe von i und j ab. Bei Zeitgleichheit gilt xi(j) = 0, sodass dieser Faktor insgesamt gleich 1 ist. Gilt für den zeitlichen Unterschied xi(j) ≥ sx, so wird der Ausdruck dagegen null und es gilt auch wi(j) = 0. Somit ist sx der maximale zeitliche Abstand, bei dem eine Wirkung von j auf i möglich ist.
Besitzen mindestens eine Verbindung keine zeitliche Lage (z.B. DRT-Wege), so kann der erste Faktor nicht auf die oben beschriebene Art bestimmt werden. Er ist dann wie folgt definiert:
- 0, falls genau eine Verbindung keine zeitliche Lage besitzt
- 1, falls beide Verbindungen keine zeitliche Lage besitzen.
Der zweite Faktor liegt zwischen 1 (bei völliger Gleichheit im Sinne von yi(j) = 0 und zi(j) = 0) und 1 - c (bei großer Verschiedenheit von i und j). Analog zu sx ist sy+ beziehungsweise sy- der maximale Zeitvorteil oder Zeitnachteil von i, bei dem eine Wirkung von j möglich ist. Entsprechendes gilt für sz hinsichtlich des Fahrpreises. Die Standardeinstellung ergibt eine Beziehung von sy- = 2sy+ und sz- = 2sz+. Durch diese Asymmetrie wird bei zwei zeitnahen Verbindungen die bessere begünstigt, da ihre Wirkung auf die schlechtere Alternative größer ist als umgekehrt. Grundsätzlich sollte deshalb immer EigKoeffQualitätHoch (EKQH) < EigKoeffQualitätGering (EKQG) gewählt werden. Bei Verletzung dieser Regel erscheint eine Warnung zu Beginn der Umlegung (oder eine Fehlermeldung im Fenster).
Insgesamt gilt Folgendes:
sx = min (2 • mittlere Wartezeit eines zufällig zugehenden Fahrgasts zwischen der ersten und der letzten Abfahrt, maximales Zeitfenster)
sy+ = EKQH • durchschnittliche ERZ im gesamten Umlegungszeitraum
sy- = EKQG • durchschnittliche ERZ im gesamten Umlegungszeitraum
sz+ = EKQH • durchschnittlicher Fahrpreis im gesamten Umlegungszeitraum
sz- = EKQG • durchschnittlicher Fahrpreis im gesamten Umlegungszeitraum
|
Hinweis: Es werden also nur die zeitliche Lage, die ERZ und der Fahrpreis verglichen, hingegen werden Verlaufsinfos nicht ausgewertet. |
Liegen keine Fahrpreise vor (das heißt FPi = 0 für alle i), setzt man sz = 1.
Nun wird das Attribut Eigenständigkeit einer Verbindung wie folgt definiert.
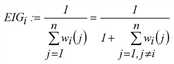 o
o
Dabei sei n die Anzahl aller Verbindungen.
Aufteilungsmodelle mit Eigenständigkeit
Bei Verwendung der Eigenständigkeit im Rahmen der Verbindungswahl muss dieses Attribut in das Aufteilungsmodell integriert werden. In der obigen Fassung wurde je Zeitintervall a der Nutzen Uia einer Verbindung i berechnet und hieraus ihr prozentualer Anteil an der Nachfrage des Zeitintervalls bestimmt. Bei Verwendung der Eigenständigkeit tritt Uia • EIGi an die Stelle von Uia, das heißt, es gilt Folgendes:
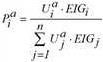
Durch diese lineare Abhängigkeit vom Eigenständigkeitsattribut ist gewährleistet, dass k zeitgleiche, identische Alternativen wie eine einzige Verbindung behandelt werden. Denn nach der Definition von EIG beträgt die Eigenständigkeit jeder dieser k Alternativen genau 1 / k (wenn nicht noch weitere zeitnahe Verbindungen Einfluss nehmen). Dadurch ist die Summe ihrer Gewichte in der Aufteilungsformel gerade gleich dem Gewicht einer einzelnen, nicht vervielfachten Verbindung derselben Art.
Vergleich der Aufteilungsmodelle mit Eigenständigkeit
In Tabelle 187 bis Tabelle 191 werden die verschiedenen Aufteilungsmodelle jeweils mit und ohne Eigenständigkeit miteinander verglichen. Die Verfahrensparameter seien wie in Tabelle 186 gewählt.
Die zum jeweils vorangehenden Beispiel abgeänderten Verbindungsdaten sind in Tabelle 187 bis Tabelle 191 fett gedruckt. Alle Umlegungsanteile sind Prozentangaben.
|
Verbindungsdaten |
Aufteilung ohne EIG |
Aufteilung mit EIG |
||||||||||
|
Nr |
Abf |
Ank |
ERZ |
FP |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
|
1 |
10 |
30 |
20 |
3,00 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
|
2 |
30 |
50 |
20 |
3,00 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
|
3 |
50 |
70 |
20 |
3,00 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
33,3 |
|
Verbindungsdaten |
Aufteilung ohne EIG |
Aufteilung mit EIG |
||||||||||
|
Nr |
Abf |
Ank |
ERZ |
FP |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
|
1 |
10 |
30 |
20 |
3,00 |
25 |
25 |
25 |
25 |
33,3 |
33,3 |
33,3 |
33,3 |
|
2 |
30 |
50 |
20 |
3,00 |
25 |
25 |
25 |
25 |
16,7 |
16,7 |
16,7 |
16,7 |
|
3 |
30 |
50 |
20 |
3,00 |
25 |
25 |
25 |
25 |
16,7 |
16,7 |
16,7 |
16,7 |
|
4 |
50 |
70 |
20 |
3,00 |
25 |
25 |
25 |
25 |
33,3 |
33,3 |
33,3 |
33,3 |
|
Verbindungsdaten |
Aufteilung ohne EIG |
Aufteilung mit EIG |
||||||||||
|
Nr |
Abf |
Ank |
ERZ |
FP |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
|
1 |
10 |
30 |
20 |
3,00 |
25 |
25 |
25 |
25 |
32,7 |
32,7 |
32,7 |
32,7 |
|
2 |
30 |
50 |
20 |
3,00 |
25 |
25 |
25 |
25 |
17,3 |
17,3 |
17,3 |
17,3 |
|
3 |
32 |
52 |
20 |
3,00 |
25 |
25 |
25 |
25 |
17,3 |
17,3 |
17,3 |
17,3 |
|
4 |
50 |
70 |
20 |
3,00 |
25 |
25 |
25 |
25 |
32,7 |
32,7 |
32,7 |
32,7 |
|
Verbindungsdaten |
Aufteilung ohne EIG |
Aufteilung mit EIG |
||||||||||
|
Nr |
Abf |
Ank |
ERZ |
FP |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
Kirchhoff |
Logit |
Box-Cox |
Lohse |
|
1 |
10 |
30 |
20 |
3,00 |
25,9 |
26,7 |
26,2 |
25,1 |
31,9 |
32,6 |
32,2 |
31,2 |
|
2 |
30 |
50 |
20 |
3,00 |
25,9 |
26,7 |
26,2 |
25,1 |
20,2 |
20,7 |
20,4 |
19,8 |
|
3 |
32 |
47 |
20 |
3,30 |
22,3 |
19,8 |
21,3 |
24,6 |
16,0 |
14,1 |
15,2 |
17,8 |
|
4 |
50 |
70 |
20 |
3,00 |
25,9 |
26,7 |
26,2 |
25,1 |
31,9 |
32,6 |
32,2 |
31,2 |
Die Tatsache, dass ohne Verwendung von Eigenständigkeit die Verbindungen 1, 2 und 4 in allen Fällen gleich viele Fahrgäste erhalten, macht deutlich, dass die Wechselwirkungen zwischen verschiedenen Alternativen hier besser berücksichtigt werden sollten. Man kann erkennen, dass dann mit allen Aufteilungsmodellen bessere Ergebnisse erzielt werden.

